|
|
 发表于 20-6-2005 09:09 PM
|
显示全部楼层
发表于 20-6-2005 09:09 PM
|
显示全部楼层
试试 Q[12]
先证右手边不等式:
(1+2+...+n) / n ≥ (1*2*...*n)^(1/n) = (n!)^(1/n)
因为 (1+2+...+n) = n(n+1) / 2 , 故右手边不等式成立.
左手边要证: n! ≥ n^(n/2), 不妨证
log 2 + ... + log n ≥ n/2 log n
这里有个用几何的概念,可是觉得不够严谨 ...
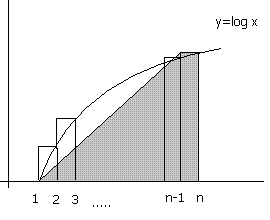
再想以下 ..
 |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 21-6-2005 09:47 AM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
|
|
 发表于 21-6-2005 12:33 PM
|
显示全部楼层
发表于 21-6-2005 12:33 PM
|
显示全部楼层
嘿,想到了。要证左手边,不妨证
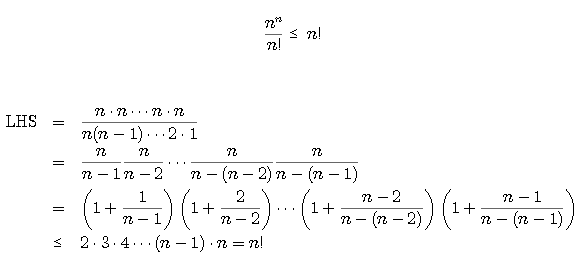
pipi 的几何解是怎么样?  |
|
|
|
|
|
|
|
|
|
|
|
 发表于 21-6-2005 03:50 PM
|
显示全部楼层
发表于 21-6-2005 03:50 PM
|
显示全部楼层
让我试试第12题 前半 部
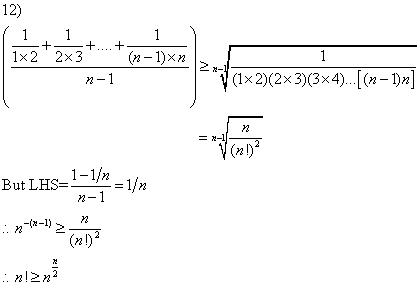
[ Last edited by dunwan2tellu on 21-6-2005 at 05:53 PM ] |
|
|
|
|
|
|
|
|
|
|
|
 发表于 21-6-2005 04:01 PM
|
显示全部楼层
发表于 21-6-2005 04:01 PM
|
显示全部楼层
15)
设S=(a-1+1/b)(b-1+1/c)(c-1+1/a)及
R=(1/c-b+1)(1/a-c+1)(1/b-a+1)
S=(a-1+1/b)(b-1+1/c)(c-1+1/a)
=(ab-b+1)(bc-c+1)(ac-c+1) 分母abc=1
=(1/c-b+1)(1/a-c+1)(1/b-a+1)=R 因 ab=1/c
这 里 要 分2 个 情 况 ,
(i) 当 S 中 的 其 中 一 个term , 说(a-1+1/b) <0 时, 必 定a<1 , b>1.
这 时,(b-1+1/c) 和 (c-1+1/a) 都 为 正 。 所 以 S < 0 <1 得 证
(ii) 当 所 有S 的term 都 为 正 时 ,
用AM-GM, (a-1+1/b)(1/b-a+1)=< (1/b)^2
(b-1+1/c)(1/c-b+1)=<(1/c)^2
(c-1+1/a)(1/a-c+1)=<(1/a)^2
所以 S^2=SxR=<(1/abc)^2
S^2=<1 得 S =< 1 证毕
[ Last edited by dunwan2tellu on 23-6-2005 at 06:26 PM ] |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 21-6-2005 06:20 PM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
|
|
 发表于 21-6-2005 09:38 PM
|
显示全部楼层
发表于 21-6-2005 09:38 PM
|
显示全部楼层
呵呵,我也来 =P
18. generalize 到
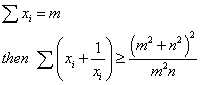
19. generalize 到
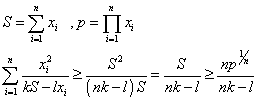 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 22-6-2005 08:58 PM
|
显示全部楼层
发表于 22-6-2005 08:58 PM
|
显示全部楼层
11)
用AM>=HM
设 1/a + 1/b >= 4/(a+b)
1/b + 1/c >= 4/(b+c)
1/c + 1/d >= 4/(c+d)
最后 1/n + 1/a >= 4/(n+a)
所以 2(1/a + 1/b +1/c ......1/n) >=4( 1/(a+b) + 1/(b+c) +1/(c+d) .....1/(n+a) )
(1/a + 1/b +1/c ......1/n) >=2( 1/(a+b) + 1/(b+c) +1/(c+d) .....1/(n+a) )
证毕 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 22-6-2005 10:48 PM
|
显示全部楼层
发表于 22-6-2005 10:48 PM
|
显示全部楼层
18)用 柯西不等试
{[a+1/a)^2+(b+1/b)^2+(c+1/c)^2}(1+1+1)
>=(1+1/a +1/b + 1/c)^2
>={1 + 9/(a+b+c)}^2
=100
19)也是用 柯西 不等试,
{x^2/(y+z)+y^2/(x+z)+z^2/(x+y)}{(y+z)+(x+z)+(x+y)}
>=(x+y+z)^2
得 原试 >=(x+y+z)/2 >=3 x cuberoot(xyz) /2 =3/2
[ Last edited by dunwan2tellu on 23-6-2005 at 05:22 PM ] |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 23-6-2005 11:53 AM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
|
|
 发表于 23-6-2005 05:19 PM
|
显示全部楼层
发表于 23-6-2005 05:19 PM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
|
|
 发表于 23-6-2005 08:01 PM
|
显示全部楼层
发表于 23-6-2005 08:01 PM
|
显示全部楼层
试这题 ,
 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 23-6-2005 08:57 PM
|
显示全部楼层
发表于 23-6-2005 08:57 PM
|
显示全部楼层
我试第20题
也用柯西不等式
[(x^3)y + (y^3)z + (z^3)x][1/xy + 1/yz + 1/xz] >= (x+y+z)^2
[(x^3)y + (y^3)z + (z^3)x] >= (x+y+z)^2 / (1/xy + 1/yz +1/xz)
>= (x+y+z)(xyz) 证毕 |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 24-6-2005 10:43 AM
|
显示全部楼层
又有新题目了(请看第 1 页, 第 1 个贴的"解说"):
 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 24-6-2005 04:39 PM
|
显示全部楼层
发表于 24-6-2005 04:39 PM
|
显示全部楼层
Question 22
Let f(x) = sin x
Then f''(x) = -sin x =< 0
So by using Jensen's Inequality
(sin A + sin B + sin C) / 3 =< sin[( A+B+C ) / 3 ]
(sin A + sin B + sin C) / 3 =< sin[ 180 / 3 ]
(sin A + sin B + sin C) =< 3(sin 60)
(sin A + sin B + sin C) =< 3 (sqrt 3) / 2
Then we get
1 / (sin A + sin B + sin C)>= 2 / 3 (sqrt 3)
Use GM >= HM
(1 / sinAsinBsinC)^1/3 >= 3 ( 1 / (sin A + sin B + sin C) )
(1 / sinAsinBsinC)^1/3 >= 2 / (sqrt 3)
(1 / sinAsinBsinC) >= 8 / 3 (sqrt 3)
sinAsinBsinC =< 3 (sqrt 3) / 8 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 24-6-2005 11:07 PM
|
显示全部楼层
发表于 24-6-2005 11:07 PM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 25-6-2005 09:38 AM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 26-6-2005 11:13 AM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
|
|
 发表于 27-6-2005 05:14 PM
|
显示全部楼层
发表于 27-6-2005 05:14 PM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 28-6-2005 09:25 AM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
| |
 本周最热论坛帖子 本周最热论坛帖子
|